摘要:定量化和精细化管理是企业发展的必由之路,燃气企业老的管理模式是从事故到事故的被动抢修模式,新的管理模式是以风险预评判为基础的无事故预防型管理。风险预评判只有建立在定量分析的水平上,才能真正具有系统性、精确性和预见性,所以管道事故数据的获取和分析是定量风险评估方法建立、改进和完善的基础。基于回归分析的方法预测管道事故率,事故率为因变量,自变量可以有很多种(管道内径、管道埋深、管壁厚度等),本文以管径为自变量从而分析出递变性的规律,从最具普遍性的损害原因(第三方损害)着手,借鉴国外(欧洲)燃气管道事故统计资料和分析方法,得出管道事故率回归方程,体现影响因素与管道事故率之间的函数关系。
关键词:城市燃气;天然气;管道事故;定量风险评估;回归分析;第三方损害;事故统计;事故率预测
1 引言
定量化和精细化管理是企业发展的必由之路,管道定量风险评估是提高管线运行经济和安全水平的重要途径[1]。风险的识别和评价基于管道事故方面的数据信息,定量风险评价技术正处在发展阶段,历史数据的发掘能够揭示事故率和事故原因之间的定量关系。
2 管道事故率统计的分类方法
管道事故率的确定是一个复杂的问题,并且有很大的不确定性,造成管道事故的原因多种多样,有的是与时间相关的(例:腐蚀、疲劳失效),有的是与时间无关的(例:第三方损坏、超压)。所以,管道事故率是设计参数、施工质量、维护措施和运行环境的函数[2]。
管道事故率的预测问题可以根据导致事故的原因分类考虑,首先从最主要事故原因着手分析无疑是行之有效的方法。国内外的天然气管道事故统计表明第三方损害是泄漏事故发生的主要原因,以往的研究结果证明第三方损害的危害程度主要受以下参数影响:埋深、壁厚、位置、保护措施。欧洲燃气管道事故数据库(European Gas pipeline Incident data Group,EGIG)报告中有较为详细的分类统计。
EGIG对于第三方损害的统计是基于以下参数分类的[3]:①管径;②管壁厚;③管道地理位置;④管道埋深;⑤管道保护措施。
需要强调的是这些管道事故的统计,管道压力≥1.5MPa,包括管径DN 100mm以下的管道。在管道事故统计的分类办法中,按管径分类可以方便的把统计结果应用于其它地区各管径系列管道的风险分析。
北京市中压以上(包括中压)天然气管道事故分类可以采用的方法有[1]:
① 按管径分类:主要包括DN 200、300、400、500、700、1000mm;
② 按埋深分类:≥1.5m(市政路)、≥1.2m:
③ 按管壁厚分类(次高压A以上):9.5mm、11.9mm:
④ 按保护措施分类:有电极保护、无电极保护、防腐层3层PE,其它防腐层。
从以上的分类来看,按埋深、壁厚和保护措施的分类形式较少,以此为基础都难以分析出递变性的规律,所以按管径分类的办法,一方面分类比较详细,另一方面可以为其它地域的统计数据引入或比较提供方便。
3 历史数据
历史数据的有效收集是进行定量风险评价的基础,也是政府和企业制定安全规范和制定风险决策的依据。现在世界上各个国家和专业技术公司都已认识到基础数据的极端重要性,已经建立起了数百种由政府和企业资助的基础数据库[4]。
欧洲燃气管道事故数据库(EGIG),包括丹麦、西班牙、比利时、芬兰、挪威、法国、德国、意大利、瑞士、英国、捷克、葡萄牙、瑞典、爱尔兰、奥地利,总计15个国家,总管长约13×104km(管道压力≥1.5MPa.包括DN 100mm以下的管道)㈣。这个数据库已经在世界各地的燃气管道安全分析中广泛应用,对提高管道安全发挥了作用。
欧洲燃气管道1970年至2007年间的统计数据根据以下泄漏的尺寸将管道破损进行分类记录[3]。
①微孔/裂纹:缺陷直径<2cm;②孔洞:2cm≤缺陷直径≤盾管道直径;③断裂:缺陷直径>管道直径。
M¼所示为EGIG第三方(外部干扰)造成的管道破损面积(事故情形)与管道内径之间的统计关系[3],横坐标为管径,纵高坐标为事故率(1000km管道在1年内发生事故的次数:次/(1000km·a))。对原始图表[3](图1)的观测发现小管径的受损率更高,这是因为较小的管径的壁厚也较小,它被刮破的可能性也更大。
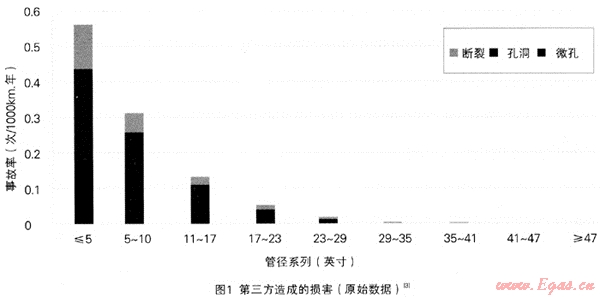
4 回归分析
为了能够利用欧洲燃气管道事故报告的数据,首先要对其报告中展示的柱状图进行数据的二次生成,原始数据显示对应相应的管径范围事故情形按破损程度分为三类:微孔、孔洞、断裂。对原始图表的数据二次生成如表1所示。利用回归分析的方法进行预测时,还需注意历史数据的适用范围,并根据现在考虑的具体情况作出相应修整,特别是有些风险事件尚未发生,事前很难对其作出准确事故发生概率预测[4]。下面所述是针对尚未发生的小概率事件而采取的弥补办法。图1仅显示了管径小于1000mm的数据,因为更大管径的事故尚未出现(事故率处在较低的水平,但并不等于零),这些缺少的数据不能直接计算得到,需要用数理统计的方法确定这些缺少的数据。欠缺数据的取值范围介于零和最后可获得数值之间,最后可获得数值是指按管径分级的数据中的最后一个管径系列的事故率观测值,大于此管径系列的其它管径事故率观测值为零,现在就是用最后可获得值代替未获得的数据[5]。
表1 第三方造成的损害——管径与事故率
|
管径范围/英寸
|
管径范围(单位转换mm)
|
事故情形分类/[次/1000km·a)
|
总计/[次/1000km·a)]
|
|||
|
下限
|
上限
|
孔洞
|
微孔
|
断裂
|
||
|
≤5
|
0+
|
127
|
O.181
|
0.257
|
0.124
|
0.562
|
|
5~10
|
127
|
254
|
0.067
|
O.190
|
0.057
|
0.314
|
|
11~17
|
279
|
432
|
0.038
|
0.071
|
O.024
|
0.133
|
|
17~23
|
432
|
584
|
0.019
|
0.024
|
O.010
|
0.052
|
|
23~29
|
584
|
737
|
0.006
|
0.008
|
0.006
|
0.020
|
|
29~35
|
737
|
889
|
—
|
—
|
0.005
|
0.005
|
|
35~41
|
889
|
1041
|
—
|
—
|
0.005
|
0.005
|
|
41~47
|
1041
|
1194
|
—
|
—
|
—
|
—
|
|
≥47
|
1194
|
1194+
|
—
|
—
|
—
|
—
|
|
注:符号“—”代表未能从原始数据中读取的数据。原始数据的管径是按英制单位分类的,这里为了便于分析,用mm对原有数据进行了转换。
|
||||||
表2显示了这种数据处理方法的结果(表中填充部分)。这种做法主要考虑欠缺数据的缺少是因为这些数值较小,在现有的运营期限内案例尚未出现,它的值介于零和最小观测值之间,取最小观测值相当于取上限值,属于按最不利情况的取值,防止统计分析的结果未能体现出可能出现的最危险状况。
表2 第三方造成的损害——管径与事故率欠缺数据的弥补
|
管径范围/英寸
|
管径范围(单位转换mm)
|
事故情形分类/[次/(1000km·a)]
|
|||
|
下限
|
上限
|
孔洞
|
微孔
|
断裂
|
|
|
≤5
|
0+
|
127
|
0.257
|
0.181
|
0.124
|
|
5~10
|
127
|
254
|
0.19
|
0.067
|
0.057
|
|
11~17
|
279
|
432
|
0.071
|
0.038
|
0.024
|
|
17~23
|
432
|
584
|
O.024
|
0.019
|
0.010
|
|
23~29
|
584
|
737
|
O.008
|
0.006
|
0.006
|
|
29~35
|
737
|
889
|
0.008
|
0.006
|
0.005
|
|
35~41
|
889
|
1041
|
0.008
|
0.006
|
0.005
|
|
41~47
|
1041
|
1194
|
0.008
|
0.006
|
0.005
|
|
≥47
|
1194
|
”94+
|
0.008
|
O.006
|
0.005
|
|
注:表中斜体是经过弥补的数据,用字框显著标出的数值是弥补时采用的数值。
|
|||||
根据表2数据以管径为自变量(横坐标),事故率为因变量(纵坐标)绘制散点图,观察散点图发现事故率与管径存在递减的函数关系,可以利用曲线线性回归分析的办法进行试算,可供选择和函数关系有:幂函数y=xa、指数函数y=ax、对数函数y=logax。经过试算发现幂函数的拟合效果最好,确定为事故率回归分析的函数类型。
回归分析就是从某一组数据出发,判断变量之间是否存在相关关系,确定它们之间的数学表达式即回归方程,并对其可信程度作统计检验。然后利用确定的回归方程进行预测和控制[6~8]。
表3 管径与第三方损害事故率
|
序号
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
管径范围/英寸
|
≤5
|
5~10
|
11~17
|
17~23
|
23~29
|
29~35
|
35~41
|
41~47
|
≥47
|
|
x管径中间值/mm
|
127
|
191
|
356
|
508
|
660
|
813
|
965
|
1118
|
1194
|
|
y事故率
/[次/(1000km·a)]
|
0.562
|
0.314
|
O.133
|
0.052
|
O 02
|
0.019
|
O 019
|
0.019
|
0.019
|
|
注:表3中第三方损害事故率是指由表2中第三方损害“微孔”、“孔洞”、“断裂”事故率的加和。
|
|||||||||
管径作为自变量,事故率则作为因变量,通过回归分析预测某一管径的管道事故率范围。管径与事故率的关系基本呈倒幂函数关系,可用下式表示:
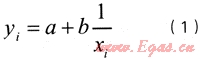
式中yi——管径系列i的事故率,次/(1000km·a)
a、b——系数
xi——第i系列管道的管径中间值,mm
建立经验回归方程的目的在于揭示两个相关变量x与y之间的内在规律,所建立的回归方程是否有意义还要经过回归显著性检验。用F检验对回归方程作显著性检验的方法称为方差分析,其检验过程可由一张方差分析表来进行[6~8],见表4,计算案例如表5所示。
表4 方差分析表
|
方差来源
|
偏差平方和
|
自由度
|
方差
|
F值
|
Fα
|
显著性
|
|
回归
|
SR
|
1
|
VR=SR/1
|
F=VR/Ve
|
F0.05(1,n-2)
|
**
|
|
剩余
|
Se
|
n-2
|
Ve=Se/(n~2)
|
—
|
F0.05(1,n-2)
|
—
|
|
总和
|
ST
|
n-1
|
—
|
|||
若F>F0.04(1,n-2),则为高度显著,在上表显著性列标“**”;F0.05(1,n-2)≤F≤F0.01(1,n-2),则为显著,在显著性栏标“*”;若F<F0.05(1,n-2)则为不显著,在显著性栏不标记号[6~8]。
ST:总的偏差平方和,它反映y1,y2,…yx只的离散程度,ST=SR+Se;
SR:回归平方和,反映了由于x的变化而引起y的波动的大小,通也对y的相关性而引起的:
Se:剩余平方和,反映出除了x对y的线性影响之外的剩余因素对y所引起的波动大小。
若回归方程有意义,即引起y波动主要是由x变化而引起的,其它一切因素是次要的,即要求SR尽可能大,而Se尽可能小。回归直线对样本数据点的拟合程度,通常用可决系数R2来表示R2=SR/ST,R2越接近于1,表明回归直线对样本数据点的拟合程度越高[6~8]。
表5 管径与第三方损害事故率方差分析表
|
方差来源
|
偏差平方和
|
自由度
|
方差
|
F值
|
Fα
|
显著性
|
|
回归
|
0.2841
|
1
|
0.2841
|
517.4457
|
5.591
|
**
|
|
剩余
|
0.0038
|
7
|
0.00054903
|
—
|
12.2464
|
—
|
|
总和
|
0.2879
|
8
|
—
|
|||
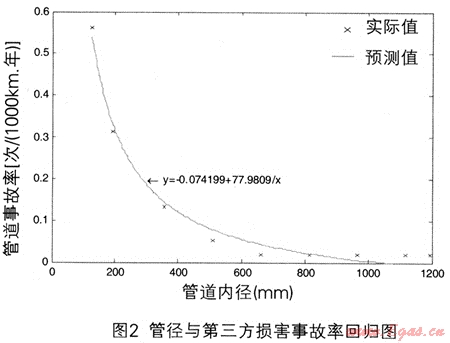
根据表5数据,通过回归分析可以得到回归方程:
y=-0.074199+77.9809/x
可决系数:R2=O.9933
F检验[F>F0.01(1,n-2)]:517.4457>5.5914;显著性:高度显著。
管径与事故率的回归方程通过了F检验与R检验,即可用来预测,所谓预测问题,就是在确定自变量的某一个X0值时求相应的变勤的估计值。第三方损害的计算结果列于表6中,回归图如图3~5所示。
表6 第三方损害一元回归分析结果
|
y事故率/[次/(1000km·a)]
|
回归方程
|
可决系数
|
F检验
F>F0.01(1,n-2)
|
显著性
F>F0.01(1,n-2)为高度显著
|
|
“微孔”破损
|
y=-0.023006+23.1641/x
|
R2=0.96777
|
103.359>5.591
|
高度显著
|
|
“孔洞”破损
|
y=-O.035285+38.4419/x
|
R2=O.98994
|
342.620>5.591
|
高度显著
|
|
“断裂”破损
|
y=-0.015763+16.3614/x
|
R2=O.98145
|
183.412>5.591
|
高度显著
|
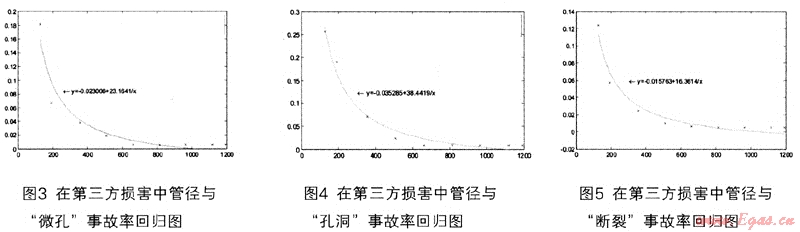
5 应用举例
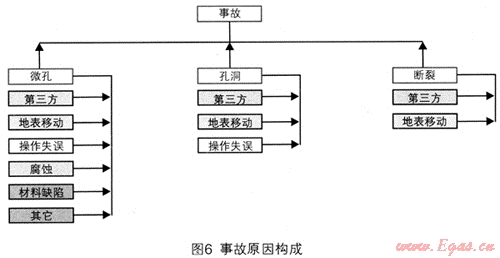
某一地区的事故原因构成如图6所示,单位管长泄漏事故的发生率用ф2表示,简称“事故率”,单位:[次/(1000km·a)]。
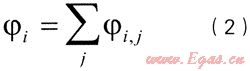
式中i——管道破损情形序号,i=1、2、3分别对应管道破损微孔、孔洞、断裂情形
j——事故原因序号,对于天然气管道泄漏事故可以按照管道破损原因进行划分;j=1,2,3……,6分别对应第三方损害、地表移动、操作失误、腐蚀、材料缺陷、以及其它未知原因。
该地区有燃气管道投入运营的年数有限,所积累的管道事故数据不足,近年来其管道运营管理水平与欧洲相似,可以利用EGIG确定出管道事故率的数量级。例如DN·500·mm的天然气管道因第三方损害发生泄漏的事故率为(利用表6中的回归方程计算,取x=500):
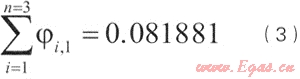
6 结语
第三方损害管道事故率的分析表明,一方面,相对来说管径越大事故率越低,这也与管道运营管理的经验相符,大管径因为机械强度更高而受损泄漏的概率更低。另一方面,管道事故数据的收集整理能够为管道的定量风险评价提供依据。
参考文献:
[1] 杜学平.北京市天然气输配管网风险评估的应用研究(硕士学位论文)[D].北京:北京建筑工程学院.2010
[2] JO Y D,BUM J A A method of quantitative risk assessment for transmission pipeline carrying natural gas[J].Journal of Materials,2005,(8)1-12
[3] European Gas pipeline Incident Data Group(EGIG).The 7th EGIG report[EB/OL]. http:/SNWW egig.nl/nav/publication.htm.2008-12
[4] 周伟国.马国彬能源工程管理[M].上海:同济大学出版社,2007
[5] MATHER J,BLACKMOREC,PETRIEA,et al An assessment of measures in use for gas pipeline to mitigate against damage third party activity[M].Norwich(United Kingdom):Health and Safety Executive(HSE),2001
[6] 刘燕,张应辉,杜学平.基于回归分析的北京市天然气供应规模预测[J].煤气与热力,2010,30(6):A26-A29
[7] 何灿芝,罗汉应用数理统计[M].长沙:湖南大学出版社,2004
[8] 王岩,隋思连,王爱青数理统计与MATLAB工程数据分析[M].北京:清华大大学出版社,2006
(本文作者:杜学平1 刘燕1 刘蓉2 1.北京市燃气集团有限责任公司 北京 100035;2.北京建筑工程学院 北京 100044)
您可以选择一种方式赞助本站

支付宝转账赞助

微信转账赞助
